מהי יחידה אסטרונומית?

Send

כשמדובר בהתמודדות עם הקוסמוס, אנו בני האדם אוהבים לשבת דברים במונחים מוכרים. בבדיקת exoplanets אנו מסווגים אותם על פי הדמיון שלהם עם כוכבי הלכת במערכת השמש שלנו - כלומר יבשתית, ענקית גז, גודל אדמה, בגודל יופיטר, בגודל נפטון וכו '. כשמדוד מרחקים אסטרונומיים אנו עושים הרבה אותו.

לדוגמה, אחד האמצעים הנפוצים ביותר למדידת מרחקים בחלל מכונה יחידה אסטרונומית (AU). בהתבסס על המרחק בין כדור הארץ לשמש, יחידה זו מאפשרת לאסטרונומים לאפיין את המרחקים העצומים בין כוכבי הלכת השמש לשמש, ובין כוכבי לכת חוץ-סולריים לכוכביהם.

הגדרה:

על פי האמנה האסטרונומית הנוכחית, יחידה אסטרונומית יחידה שווה ל 149,597,870.7 ק"מ (או 92,955,807 מיילים). עם זאת, זהו המרחק הממוצע בין כדור הארץ לשמש, מכיוון שהמרחק הזה נתון לשונות בתקופת מסלול כדור הארץ. במילים אחרות, המרחק בין כדור הארץ לשמש משתנה במהלך שנה אחת.

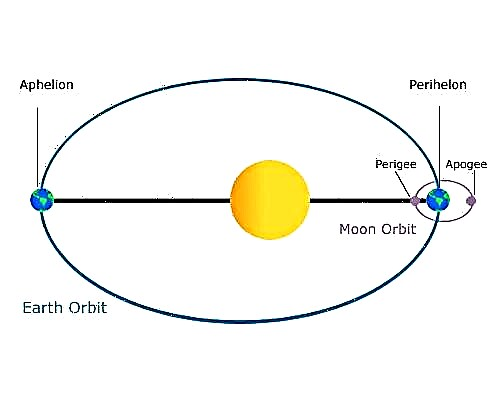
במהלך שנה כדור הארץ עובר ממרחק של 147,095,000 ק"מ (91,401,000 מיילים) מהשמש perihelion (הנקודה הקרובה ביותר שלה) ל 152,100,000 ק"מ (94,500,000 מייל) באפיליון (הנקודה הרחוקה ביותר שלו) - או ממרחק של 0.983 AUs ל 1.016 AUS.

היסטוריה של התפתחות:

הדוגמה המוקדמת ביותר של אסטרונומים המעריכים את המרחק בין כדור הארץ לשמש, מתקופת העתיקה הקלאסית. במאה ה -3 לפנה"ס, בגדלים ובמרחקים של השמש והירח - שמיוחס למתמטיקאי היווני אריסטארכוס מסאמוס - הערכה כי המרחק היה בין 18 ל -20 פי המרחק בין כדור הארץ לירח.

עם זאת, ארכימדס עכשווי שלו, במאה ה -3 לפני הספירה Sandreckoner, כמו כן טען כי אריסטארכוס מסמוס הציב את המרחק פי 10,000 מרדיוס כדור הארץ. תלוי בערכים של כל אחת מהערכות, אריסטארכוס הושבת על ידי גורם של בערך 2 (במקרה של רדיוס כדור הארץ) ל 20 (המרחק בין כדור הארץ לירח).

הטקסט המתמטי הסיני העתיק ביותר - המאה הראשונה לפנה"ס המכונה ג'ובי סואנג'ינג- מכיל גם אומדן למרחק בין כדור הארץ לשמש. על פי המסמך האנונימי, ניתן לחשב את המרחק על ידי ביצוע מדידות גיאומטריות באורך הצללים בשעות הצהריים שנוצרו על ידי חפצים המרוחקים במרחקים ספציפיים. עם זאת, החישובים התבססו על הרעיון שכדור הארץ היה שטוח.

המתמטיקאי והאסטרונום תלמי המפורסם מהמאה השנייה לסה"נ הסתמך על חישובים טריגונומטריים כדי להגיע לאומדן מרחק השווה פי 1210 לרדיוס כדור הארץ. בעזרת תיעוד של ליקויי ירח, הוא העריך את קוטרו של הירח לכאורה, כמו גם את הקוטר הנראה של חרוט הצל של כדור הארץ שחצה הירח במהלך ליקוי ירח.

באמצעות הפרלקס של הירח, הוא גם חישב את הגדלים לכאורה של השמש והירח והגיע למסקנה שקוטר השמש שווה לקוטר הירח כאשר האחרון היה במרחק הכי גדול מכדור הארץ. מכאן הגיע תלמי ליחס בין מרחק השמש לירח של בערך 19-1, אותה דמות שמקורה אריסטארכוס.

במשך אלף השנים הבאות, ההערכות של תלמי על מרחק כדור הארץ-שמש (בדומה לרוב משנתו האסטרונומית) יישארו קאנונים בקרב אסטרונומים אירופאים ואיסלאמיים מימי הביניים. רק במאה ה -17 החלו האסטרונומים לשקול מחדש ולעבד את חישוביו.

הדבר התאפשר הודות להמצאת הטלסקופ, כמו גם לשלושת חוקי התנועה הפלנטרית של קפלר, שסייעו לאסטרונומים לחשב את המרחקים היחסיים בין כוכבי הלכת לשמש בדיוק רב יותר. על ידי מדידת המרחק בין כדור הארץ לשאר כוכבי הלכת הסולאריים, אסטרונומים הצליחו לבצע מדידות פרלקס כדי להשיג ערכים מדויקים יותר.

עד המאה ה -19, קביעות לגבי מהירות האור וקביעת סטיית האור הביאו למדידה ישירה ראשונה של מרחק כדור הארץ-שמש בקילומטרים. עד שנת 1903 נעשה שימוש לראשונה במונח "יחידה אסטרונומית". ולאורך כל המאה ה -20, המדידות נעשו מדויקות ומתוחכמות יותר ויותר, בין השאר בזכות תצפיות מדויקות על השפעות תורת היחסות של איינשטיין.

שימוש מודרני:

בשנות השישים של המאה העשרים התפתחות מדידות מכ"ם ישירות, טלמטריה ובחינת מערכת השמש באמצעות בדיקות חלל הובילו למדידות מדויקות של מיקום כוכבי הלכת הפנימיים וחפצים אחרים. בשנת 1976 אימץ האיחוד האסטרונומי הבינלאומי (IAU) הגדרה חדשה במהלך האסיפה הכללית ה -16 שלהם. כחלק ממערכת הקבועים האסטרונומיים שלהם, ההגדרה החדשה קבעה:

"היחידה האסטרונומית של אורך היא האורך (A) שעבורו קבוע הכבידה של גאוס (k) לוקח את הערך 0.01720209895 כאשר יחידות המדידה הן היחידות האסטרונומיות של אורך, מסה וזמן. הממדים של k² הם אלה של קבוע הכבידה (G), כלומר, L³M^-1ט^–². המונח "מרחק יחידה" משמש גם לאורך A. "

בתגובה לפיתוח מדידות היפר-מדויקות, הוועדה הבינלאומית למשקולות ומדידות (CIPM) החליטה לשנות את מערכת היחידות הבינלאומית (SI) בשנת 1983. בהתאם לכך, הן הגדירו מחדש את המונה למדידה במונחים של מהירות האור בוואקום.

עם זאת, עד שנת 2012, IAU קבעה כי השוואת היחסות הפכה את מדידת ה- AU למורכבת מדי, והגדירה מחדש את היחידה האסטרונומית מבחינת מטרים. בהתאם לכל זה, AU יחיד שווה ל 149597870.7 ק"מ בדיוק (92.955807 מיליון מיילים), 499 שניות אור, 4.8481368 × 10^-6 של פרסק, או 15.812507 × 10^-6 של שנת אור.

כיום משתמשים ב- AU בדרך כלל למדידת מרחקים וליצירת מודלים מספריים עבור מערכת השמש. הוא משמש גם למדידת מערכות חוץ-סולאריות, בחישוב היקף העננים הפרוט-פלנטריים או המרחק בין כוכבי לכת חוץ-סולאריים לכוכב האם שלהם. כשמדדים מרחקים בין-כוכביים, מחירי ה- AU קטנים מכדי להציע מדידות נוחות. ככאלה, מסתמכים על יחידות אחרות - כמו הפרסק ושנת האור.

היקום הוא מקום ענק, ומדידת אפילו הפינה הקטנה שלנו בו מניבה תוצאות מדהימות. אך כמו תמיד, אנו מעדיפים לבטא אותם בדרכים שאינן קשורות ומוכרות.

כתבנו מאמרים מעניינים רבים על מרחקים במערכת השמש כאן במגזין החלל. להלן כמה רחוק כוכבי הלכת מהשמש ?, כמה רחוק מרקורי מהשמש ?, כמה רחוק נוגה מהשמש?, כמה רחוק כדור הארץ מהשמש ?, כמה רחוק מאדים מהשמש ?, כמה רחוק הוא יופיטר מהשמש ?, כמה רחוק שבתאי מהשמש ?, כמה רחוק אוראנוס מהשמש ?, כמה רחוק נפטון מהשמש ?, כמה רחוק פלוטו מהשמש?

אם תרצה לקבל מידע נוסף על מסלול כדור הארץ, עיין בדף חקר מערכות השמש של נאס"א.

הקלטנו גם פרק של אסטרונומיה קאסט המוקדש למדידת המרחקים באסטרונומיה. האזינו כאן, פרק 10: מדידת מרחק ביקום.

מקורות: