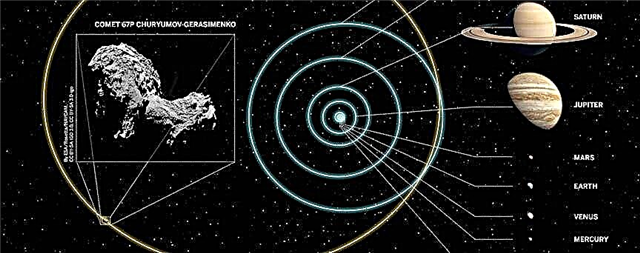
חוש הפיזיקה שלי אומר לי שמהירות הניתוק היא מהירות הבריחה.
צמצום זה עשוי לעבוד טוב יותר ביחס לשינוי האנרגטי הכולל של מערכת האסטרואידים בתוספת חומר שנפלט לאנרגיה של החומר שנפלט. משוואת הרקטות עוזרת מעט. משוואת הרקטות היא שימור של תוצאת המומנטום עם
d (mv) / dt = 0 -> (m -? m) (v +? v) -? mV = 0
כאשר V הוא מהירות מסת התגובה, V ו-? M הוא השינוי במהירות ואובדן המסה של "הרקטה", או במקרה זה האסטרואיד, ו- m ו- v הם המסה והמהירות הראשונית של העצם. קבענו v = 0 ומקבלים
? v = V (? m / m)
והמהירות המשולבת למעלה היא v = V ln (m_i / m_f), עבור m_i המסה ההתחלתית ו- m_f המסה הסופית. אם השינוי במסה הוא קטן שיש לנו
v ~ = V (m_i / m_f - 1)
ותנופת האסטרואיד בסוף היא p ~ = V (m_i - m_f). אנו נותנים כעת ל- V = u - v_e, עבור v_e את מהירות הבריחה ואת u את מהירות האובייקט המורחק. משמעות הדבר היא ש- V היא מהירות האובייקט המורחק "באינסוף."
כעת נניח שאנחנו רוצים למזער את האנרגיה הקינטית של האסטרואיד K = (1/2) p ^ 2 / m_f עבור הוצאת אנרגיה קינטית מסוימת E = (1/2)? Mu ^ 2. אנו בונים יחס חסר ממדים,
R = p ^ 2 / m_f / (? Mu ^ 2 / = (p / u) ^ 2 / (? Mm_f) = (? M / m_f) (1 - v_e / u) ^ 2.
BTW, חשוב לעבוד עם יחס חסר ממדים. אז אנו ממזערים זאת עבור נתון? M ומחושבים את ה- u. אז אנחנו ממזערים
F (u) = (1 - v_e / u) ^ 2, -> dF (u) / du = -2 (1 - v_e / u) * v_e / u ^ 2,
וזה אפס ב- v_e = u. זה נראה קצת מוזר בהתחשב בנוסחת משוואת הטילים, אבל אדון בזה בהמשך.
לאחר מכן ניקח את הנגזרת השנייה כדי לקבוע אם זהו מקסימום או דקה ואנחנו מקבלים
d ^ 2F (u) / du ^ 2 = 4 (1 - v_e / u) * (v_e / u ^ 2) ^ 2 - 2 (v_e / u ^ 2) ^ 2
אשר ב- u = v_e הוא -2 <0 ולכן זהו דקה, מה שאנחנו רוצים. ברור גם כי u = v_e הוא האנרגיה הקינטית המינימלית שאנחנו יכולים להקנות למסה.
נשמע מוזר שיש לנו v ~ = V (m_i / m_f - 1), שעבור V = u - v_e הוא אפס ב- u = v_e. עם זאת, עבור u = v_e האסטרואיד יוצא החוצה עד שהאובייקט המורחק מגיע לאינסוף. המטרה לעשות זאת היא ליצור תזוזה של האסטרואיד, וככל שהאובייקט המורחק יגיע ל"אינסוף ", האסטרואיד יגיע למרחק עקירה משם.
LC